Quaternions

Tentativa de uma simples explicação sobre quaternions. Se é que é possível ser simples ao se falar de quaternions.

História

Quaternions são números quadridimensionais e foram descobertos/criados em 1843 por Hamilton. Esses números estendem os sistemas dos números complexos, onde 3 dos seus 4 eixos são imaginários. Isto é, enquanto que nos números complexos apenas 1 dos 2 eixos é imaginário (o outro continua sendo um eixo real), nos quaternions há 3 eixos imaginários e 1 real. Na matemática os quaternions são representados como \(q = a + b i + c j + d k\), onde \(i^2 = j^2 = k^2 = -1\). Logo depois foram descobertas suas propriedades de descrição de rotações espaciais.¹

Rotações

Rotação é conceito geométrico capaz de descrever movimento de corpos rígidos em torno de um ponto. É possível descrever rotações de corpos livres no espaço tridimensional decompondo a rotação em três rotações em torno de cada eixo \(x,y,z\). O ângulo de rotação em torno do eixo \(x\) é chamado de \(roll\), em torno do eixo \(y\) é chamado de \(pitch\) e \(z\) é chamado de \(yaw\).

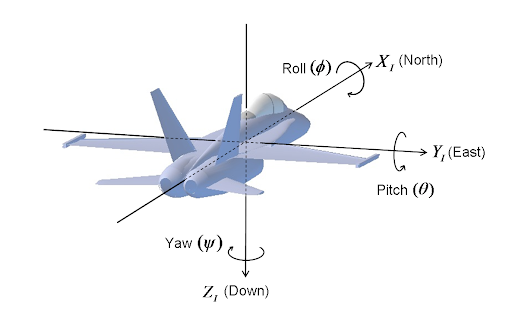
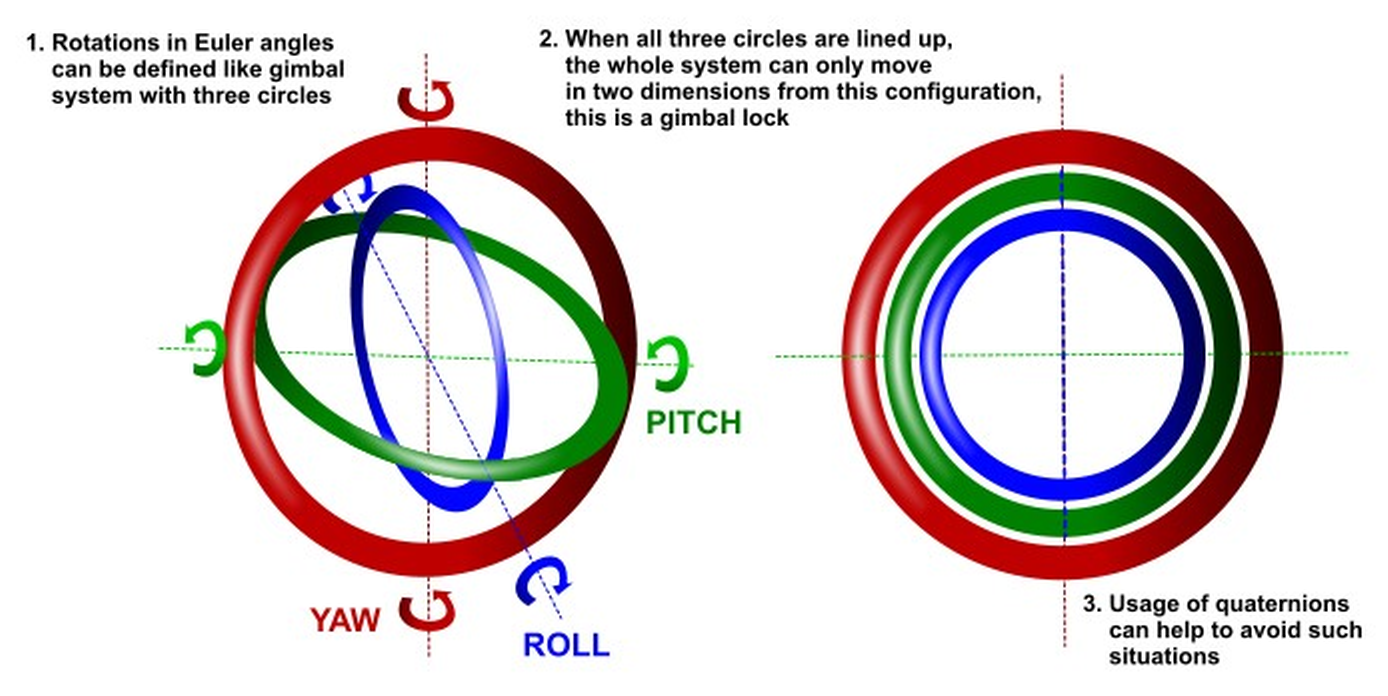
Esses ângulos são chamados de Ângulos de Euler. Contudo, existe um problema muito comum ao usar esses ângulos para calculos de movimentação de corpos que é o problema do Gimbal Lock, onde um grau de liberdade é perdido durante o controle. Por conta disso matrizes de rotação foram o padrão de uso para controle de orientação de satélites, robôs, aviões, etc. Em meados do século XX, computadores digitais dominaram esses sistemas e matrizes de rotação ficaram bastante caras em tais sistemas. Os quaternions foram, então, resgatados, pois suas rotações não são sucetíveis ao problema de Gimbal Lock e são em geral mais baratos de computar. Uma rotação 3D em quaternions tem 4 parâmetros, enquanto são 9 parâmetros nas matrizes de rotação.

Quaternions Unitários

Entretanto, não são todos os quaternions que são capazes de descrever rotações. Apenas os quaternions unitários fazem isso. Isso que apenas quaternions com norma unitária descrevem rotações espaciais. A norma de um quaternion é calculada como a norma de vetor qualquer, isto é, é possível saber se um quaternion é unitário calculando o “Pitágoras” do quaternion. Por exemplo, a norma do quaternion \(q = a + b i + c j + d k\) é calculada com a seguinte fórmula:

\( \lVert q \rVert = \sqrt{a^2 + b^2 + c^2 + d^2} \)

Se \( \lVert q \rVert = 1 \), então o quaternion é unitário. Logo, o quaternion \(q_0 = 5 + 4 i + 3 j + 2 k\) não é unitário, enquanto que o \(q_1 = 1 + 0 i + 0 j + 0 k\) é.²

Computação

O uso de quaternions dentro de computadores é mais fácil. Quaternions geralmente são implementados como um vetor simples de 4 elementos ou estrutura com um 1 float representando a parte real e um vetor com 3 floats representando a parte imaginária.

ROS

O ROS usa bastante os quaternions no transporte de mensagens por serem uma estrutura mais barata que uma matriz de rotação. Contudo, dentro da biblioteca de álgebra linear e transformadas do ROS, a tf, quaternions são transformados em matrizes de rotação na grande maioria dos cálculos. É importante salientar que para robôs que se movimentam em ambientes planares como o Pioneer e o Turtlebot, apenas a rotação em torno do eixo \(z\) é importante e por conta disso esses robôs não sofrem do problema do Gimbal Lock. Assim, é possível fazer todos os cálculos usando apenas o ângulo \(yaw\). A biblioteca tf tem funções que retiram o \(yaw\) do quaternion de orientação como pode ser visto em ³ e ⁴.

Desvantagens

Como já é possível perceber a principal desvantagens de se usar quaternions é perca de visão da rotação que o quaternion representa. Por serem números quadridimensionais é impossível vê-los, portanto um quaternion sozinho não significa nada para humanos. Geralmente, é usado sistemas auxiliares que convertem quaternions para outras formas de representação, assim humanos são capazes debugar problemas na implementação de tais sistemas. Outra desvantagem é que os quaternions são redundantes, isto é, para cada rotação 3D existem dois quaternions diferentes que representam essa rotação. Por fim, mesmo tendo apenas 4 parâmetros os quaternions não são a representação mais minimalista possível. A menor representação possível de uma rotação 3D são os ângulos de Euler, pois apenas 3 parâmetros são necessários, contudo, por conta dos problemas já mencionados são pouquíssimos usados.

Referências

1. https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation ↩

2. A Beginners Guide to Dual-Quaternions: What They Are, How They Work, and How to Use Them for 3D Character Hierarchies ↩

3. https://answers.ros.org/question/41233/how-to-understand-robot-orientation-from-quaternion-yaw-angle/ ↩

4. https://answers.ros.org/question/69754/quaternion-transformations-in-python/ ↩